Embedding ottimale e fluttuazioni statistiche
Abbiamo studiato le proprietà statistiche di una delle metriche più rilevanti nel campo della dinamica non-lineare, e cioè il massimo esponente di Lyapunov (MEL). Il MEL è valutato come il rate di divergenza delle traiettorie vicine calcolato attraverso il cosiddetto time-dependent divergence exponent. Dato un sistema, i metodi di embedding sono spesso classificati in base a quanto tali valori di MEL si avvicinano al vero MEL. Abbiamo studiato la dipendenza del MEL dai parametri di embedding sviluppando un algoritmo completamente automatico che fornisce il rate di divergenza e la sua incertezza statistica. Abbiamo mostrato che la ricerca di un embedding ottimale è viziata dalle fluttuazioni statistiche che si verificano nella stima del MEL. Questi risultati sono stati pubblicati in:
M. Franchi and L. Ricci, Statistical properties of the maximum Lyapunov exponent calculated via the divergence rate method, Phys. Rev. E 90 (2014), 062920, doi:10.1103/PhysRevE.90.062920

Un nuovo approccio all'embedding ottimale
Abbiamo sviluppato un nuovo metodo per l'identificazione di parametri di embedding adeguati. A differenza della gran parte degli approcci convenzionali, che ricercano un singolo valore ottimale per m e L per effettuare l'embedding di una sequenza temporale, il nostro approccio fornisce un insieme di scelte di embedding che sono equivalentemente adatte a ricostruire la dinamica. L'adeguatezza di ciascuna scelta di embedding m, L è verificata sulla base di test statistici, fornendo così un criterio che non richiede la valutazione soggettiva dei risultati. Il metodo è stato applicato con successo a serie temporali sintetiche e sperimentali, fornendo un nuovo punto di vista sull'annoso problema dell'embedding ottimale. Per esempio, il ruolo centrale della finestra di embedding (m-1)L, i.e. l'intervallo temporale coperto da ogni vettore di embedding, è insito nel nostro approccio. In aggiunta, il nostro metodo fornisce informazioni sull'adeguatezza del periodo di campionamento utilizzato per registrare la serie temporale. Questo nuovo approccio è stato descritto in:
A. Perinelli and L. Ricci, Identification of suitable embedding dimensions and lags for time series generated by chaotic, finite-dimensional systems, Phys. Rev. E 98 (2018), 052226 doi:10.1103/PhysRevE.98.052226
Un migliore stimatore della dimensione di correlazione
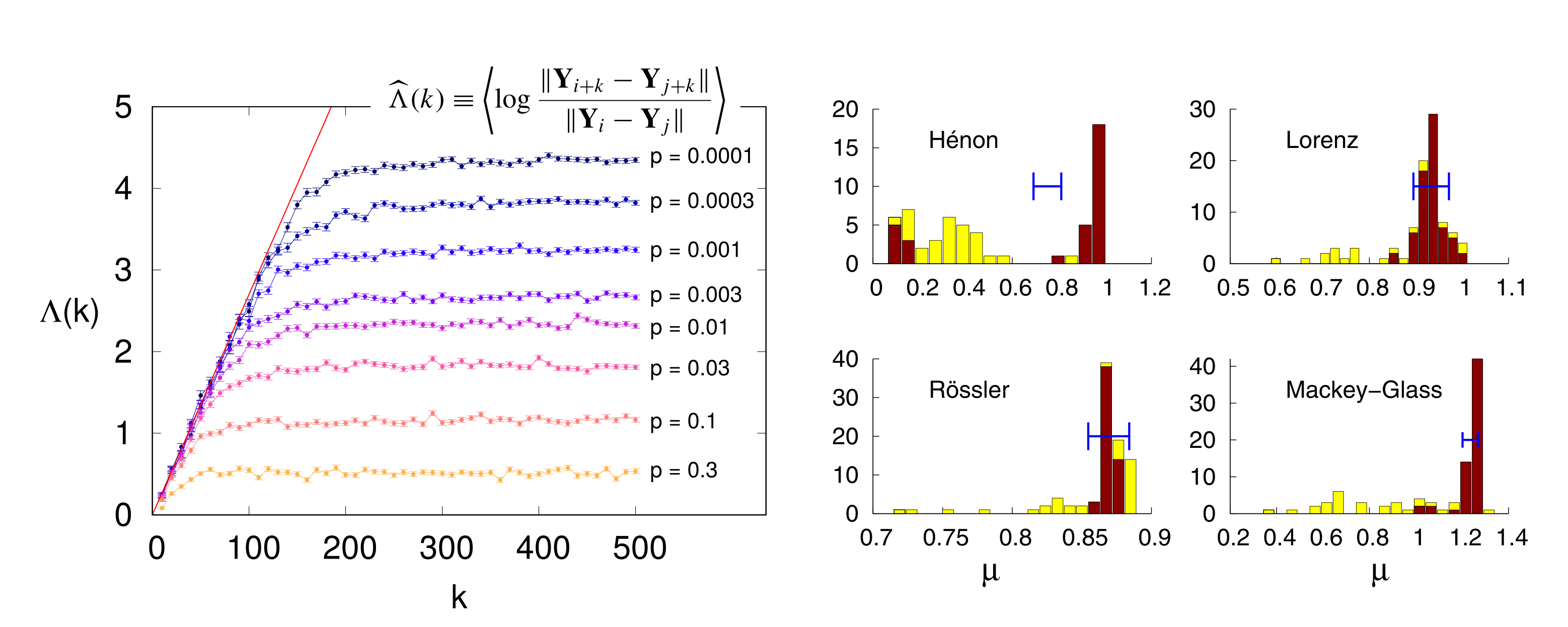
Un'altra problematica di lungo corso nell'analisi di serie temporali nonlineari è quella di distinguere il rumore dal caos. A tal fine, si possono ottenere molte informazioni analizzando il (solitamente ignorato) regime asintotico (tempi lunghi) del time-dependent divergence exponent. In particolare, la dipendenza funzionale del divergence exponent dal percentile p delle distanze utilizzato per calcolarlo è diversa nel caso di una sorgente caotica o stocastica. Oltretutto, nel caso di sorgenti caotiche, questa analisi fornisce anche una stima precisa della dimensione di correlazione del sistema. Questi risultati sono stati pubblicati in:
L. Ricci, A. Perinelli and M. Franchi, Asymptotic behavior of the time-dependent divergence exponent, Phys. Rev. E 101 (2020), 042211, doi:10.1103/PhysRevE.101.042211


A caccia di caos in dati sperimentali
Tutti i pezzi del puzzle presentati qui sono stati messi insieme disegnando così un approccio alternativo al problema di identificare il caos. Il nucleo del nuovo approccio è l'analisi di una serie temporale su un reticolo discreto di scelte dei parametri di embedding il cui risultato fornisce, se esiste, evidenza di una sorgente finito-dimensionale e caotica che genera la sequenza e, se tale evidenza è presente, restituisce un insieme di scelte di embedding equivalentemente adatte a ricostruire la dinamica. L'applicazione del metodo a due case studies sperimentali, nello specifico un circuito elettronico e dati di magnetoencefalografia di un cervello umano, evidenzia come esso sia un potente strumento per l'identificazione del caos in sistemi complessi. Il nuovo approccio è discusso in:
A. Perinelli and L. Ricci, Chasing chaos by improved identification of suitable embedding dimensions and lags, Chaos 30 (2020), 123104, doi:10.1063/5.0029333
Implementazione elettronica di un sistema caotico
Un problema cruciale nelle scienze nonlineari è rivelare il caos in dati sperimentali. Il Minimal Universal Model del caos, proposto in un recente lavoro, è stato qui implementato su un circuito stampato, con controllo digitale dei parametri del modello. Grazie ad una relazione trovata tra l'emergenza di spike e il massimo esponente di Lyapunov, sono state selezionate diverse configurazioni dei parametri che suggeriscono la presenza di caos. La prova definitiva è stata trovata usando il metodo del divergence exponent sulle serie sperimentali, fornendo valori del massimo esponente di Lyapunov in ottimo accordo con le previsioni teoriche. Questi risultati sono pubblicati in:
L. Ricci, A. Perinelli, M. Castelluzzo, S. Euzzor, R. Meucci, Experimental evidence of chaos generated by a Minimal Universal Oscillator Model, Int. J. Bifurcation and Chaos 31 (2021), 2150205, doi:10.1142/S0218127421502059
